损失函数(Loss Function)

1. 损失函数

简单来说，训练模型表示通过有标签样本来学习（确定）所有权重和偏差的理想值。在监督式学习中，机器学习算法通过以下方式构建模型：检查多个样本并尝试找出可最大限度地减少损失的模型；这一过程称为经验风险最小化。

损失是预测值与真实者的不一致程度。如果模型的预测完全准确，则损失为零，否则损失会较大。训练模型的目标是从所有样本中找到一组平均损失“较小”的权重和偏差。例如，图 3 左侧显示的是损失较大的模型，右侧显示的是损失较小的模型。关于此图，请注意以下几点：

  • 红色箭头表示损失量。
  • 蓝线表示线性预测函数。

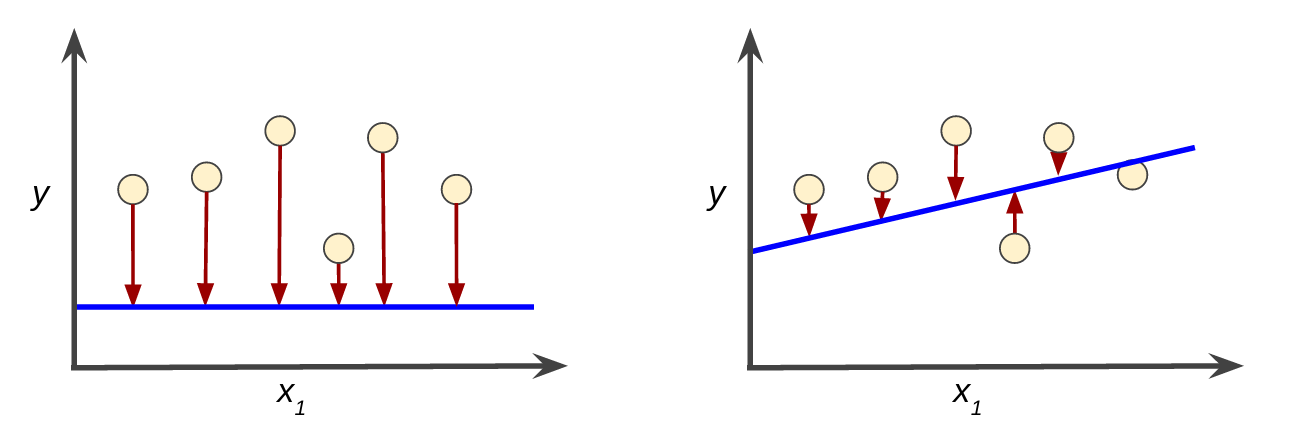
两个直角坐标曲线图，每个曲线图显示一条线和一些数据点。在第一个曲线图中，线与数据极其不吻合，所以损失较大。在第二个曲线图中，线与数据比较吻合，所以损失较小。

图 3. 左侧模型的损失较大；右侧模型的损失较小。

 

请注意，左侧曲线图中的红色箭头比右侧曲线图中的对应红色箭头长得多。显然，相较于左侧曲线图中的蓝线，右侧曲线图中的蓝线代表的是预测效果更好的模型。

您可能想知道自己能否创建一个数学函数（损失函数），以有意义的方式汇总各个损失。

均方误差：一种常见的损失函数

接下来我们要看的线性回归模型使用的是一种称为均方误差（又称为 L2 损失）的损失函数。单个样本的平方损失如下：

  = the square of the difference between the label and the prediction
  = (observation - prediction(x))2
  = (y - y')2

均方误差 (MSE) 指的是每个样本的平均平方损失。要计算 MSE，请求出各个样本的所有平方损失之和，然后除以样本数量：

$$ MSE = \frac{1}{N} \sum_{(x,y)\in D} (y - prediction(x))^2 $$

其中：

  • \((x, y)\) 指的是样本，其中
    • \(x\) 指的是模型进行预测时使用的特征集(iris花萼长度、花萼宽度、花瓣长度、花瓣宽度)。
    • \(y\) 指的是样本的标签集（iris的种类iris-setosa, iris-versicolour, iris-virginica）
  • \(prediction(x)\) 指的是权重和偏差与特征集 \(x\) 结合的函数。
  • \(D\) 指的是包含多个有标签样本（即 \((x, y)\)）的数据集。
  • \(N\) 指的是 \(D\) 中的样本数量。

损失函数除了 MSE还有交叉熵。

 

2. 线性回归，通过GeoGebra工具体验计算均方差损失

任务1：手动调整参数

$$ S = \sum_{i=1}^n (y^i - y)^2 $$

下图有5个坐标点，对5个坐标点进行\(y = ax + b \) 回归拟合, 采用最小二乘法计算，求解\(S\) 最小值。

  • 1.逐渐改变截距(y intercept)值，看\(S\) 值的变化，达到最小值。(用鼠标或键盘箭头左右键)
  • 2.然后，在逐渐改变斜率(slop)值，看\(S\) 值的变化，达到最小值。(用鼠标或键盘箭头左右键)
  • 3.重复以上步骤，探究最小值的回归方式：\(y = ax + b \)
  • 4.记录本小组得到方程参数（以上步骤可以通过矩形区域面积和进行目测）。
    • 任务2：工具线性拟合
  • 5.通过系统菜单自动的最佳拟合直线，获得方程式的参数，进行对比。

    • 拓展：观看讲解视频

    本视频来自谷歌机器快速学习微课程。视频交互支持可以支持切换语言，包括脚本所用文本和讲解所有的语言。

    机器学习损失函数